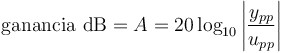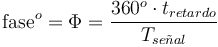Obtención experimental del diagrama de Bode

Características de la práctica

Duración

Dos horas aproximadamente.

Objetivos

El objetivo de esta práctica es obtener el diagrama de Bode experimental de un sistema (módulos electrónicos de prácticas) mediante la técnica de barrido frecuencial

Requisitos previos

• Venir a la práctica con el siguiente material:
  • Calculadora científica (es decir, con funciones trigonométricas y logarítmicas)
  • Hoja de resultados impresa (tabla de resultados numéricos y plantilla de Bode)

• Haber estudiado los siguientes conceptos básicos:
  • Respuesta en frecuencia (Franklin, 6.1).
  • Técnicas de trazado del diagrama de Bode (Franklin, 6.1.1)

• Además, para realizar adecuadamente esta práctica es conveniente:
  • Conocer los principios básicos de manejo de un osciloscopio. Puede ayudar la siguiente información Introducción al manejo del osciloscopio
  • Conocer las características de los equipos de prácticas. En la página Introducción al los módulos de prácticas puedes encontrar una descripción resumida.

Introducción. La técnica de barrido frecuencial

Esta técnica se basa en el hecho de que un sistema LTI (lineal e invariante en el tiempo) responde de manera distinta (con distintas ganancias y desfases) para senoides de distintas frecuencias.

Respuesta Frecuencial de un sistema de segundo orden (pinchar aquí para ver video)

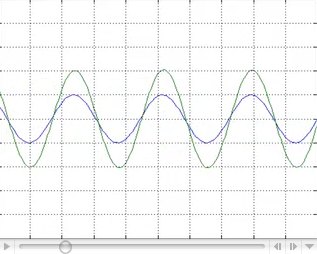
La respuesta en frecuencia, es decir, forma en la que el sistema varía su ganancia y desfase en función de la frecuencia, define unívocamente su dinámica, al igual que lo hacen la respuesta impulsional o la función de transferencia, por lo que la representación gráfica de la respuesta en frecuencia es como una "radiografía" de su dinámica. De hecho, un sistema LTI de función de transferencia L(s), tiene una ganancia |L(jω) | y produce desfase arg{L(jω)} ante senoides de frecuencia ω

Para obtener experimentalmente la respuesta en frecuencia de un sistema seguiremos el siguiente procedimiento:

• inyectamos señales senoidales a distintas frecuencias,
• determinamos las ganancias y desfases que produce el sistema a dichas frecuencias por comparación de las senoides de salida y entrada,
• finalmente representamos los puntos (y los unimos) en dos diagramas logarítmicos (uno para amplitudes y otro para fases) que constituyen el llamado diagrama de Bode.

Procedimiento básico

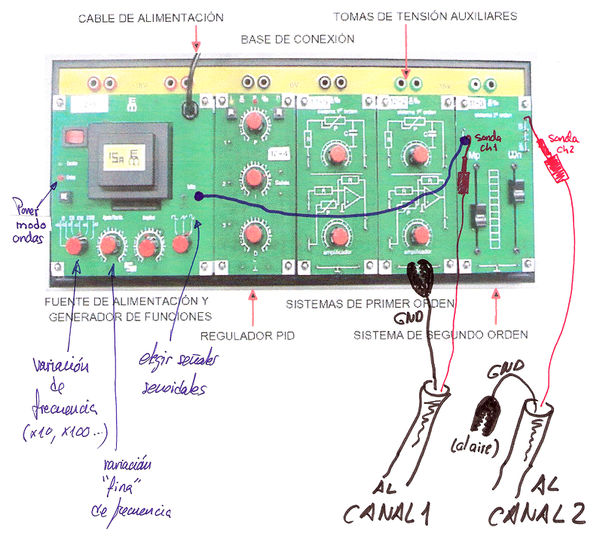
Conexión

Aplicar al sistema una entrada senoidal a frecuencia w (ver Introducción al los módulos de prácticas). Se recomienda tener en cuenta los siguientes puntos:

• Poner el generador de ondas en modo ondas
• Poner el selector de forma de onda en senoidal
• El ajuste grueso de frecuencia permite multiplicar/dividir por 10 la frecuencia en cada paso.
• El ajuste fino permite modificar la frecuencia entre dos pasos del ajuste grueso
• Una de las masas del osciloscopio debe estar conectada a la masa del equipo (la otra conviene ponerla al aire, porque internamente están conectadas)
• Conectar la salida del generador de ondas a la entrada del sistema que se va a analizar.
• Conectar las sondas de los canales 1 y 2 a la entrada y la salida del sistema, respectivamente.
• Poner el osciloscopio en modo DUAL para visualizar ambas senoides simultáneamente en el osciloscopio (ver Introducción al manejo del osciloscopio)
• Ajustar la base de tiempos para que quepa 1 ciclo de cada senoide. Si ponemos más ciclos perdemos precisión (sale más pequeño) y si ponemos menos (medio ciclo) podemos perder una parte importante para medir.
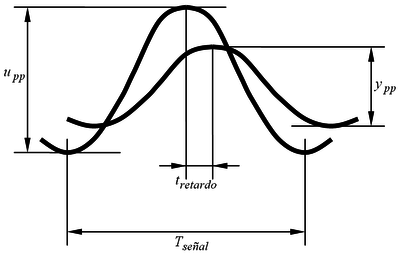
• Ajustar las bases de tensión para que las señales sean lo más grandes posibles en la pantalla. De esta manera los errores de medida serán mínimos.
• Medir siempre de pico a pico (nunca medir de cero a pico, porque si la señal está descentrada falsearemos la medida)

Como ejemplo, consultar el croquis de conexiones adjunto.

Ejemplo: croquis de conexiones para el análisis del sistema de segundo orden.

Cálculo de la ganancia y desfase

Para una frecuencia dada w, la ganancia en dB y el desfase en grados vienen dados por:

$\mbox{ganancia dB} = A = 20 \log_{10} \left|\frac{y_{pp}}{u_{pp}}\right|$ $\mbox{fase}^o = \Phi = \frac{360^o \cdot t_{retardo}}{T_{se\tilde nal}}$

Transcripción de los valores calculados al diagrama de Bode

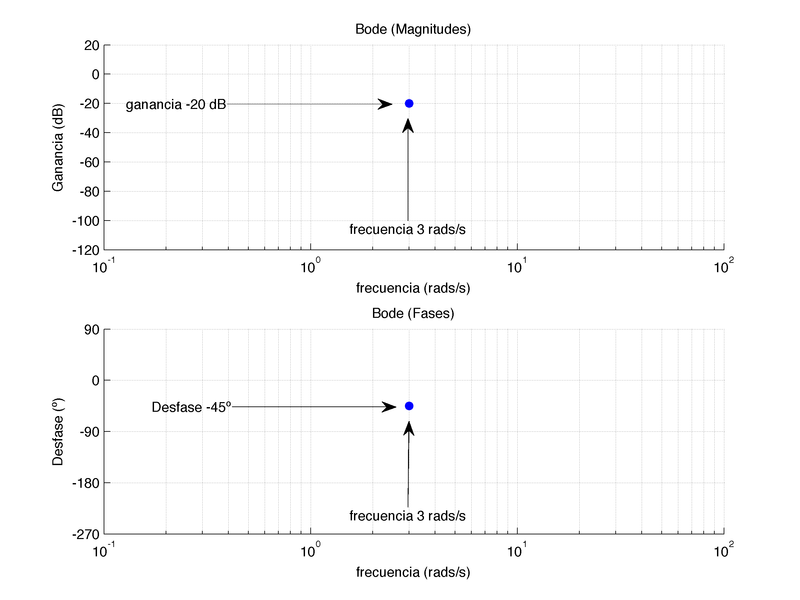
Para cada frecuencia w, se obtiene un punto del diagrama de Bode. Dado que para cada frecuencia se calculan dos valores (ganancia en dB y fase en º), en realidad se dibuja el punto en dos gráficas: la curva de magnitudes (ganancias) y la curva de fases. Por ejemplo, si para una frecuencia de 3 rads/s nos salió una ganancia de -20 dB y un desfase de -45º, el punto se anotará como sigue:

Cálculo iterativo a distintas frecuencias

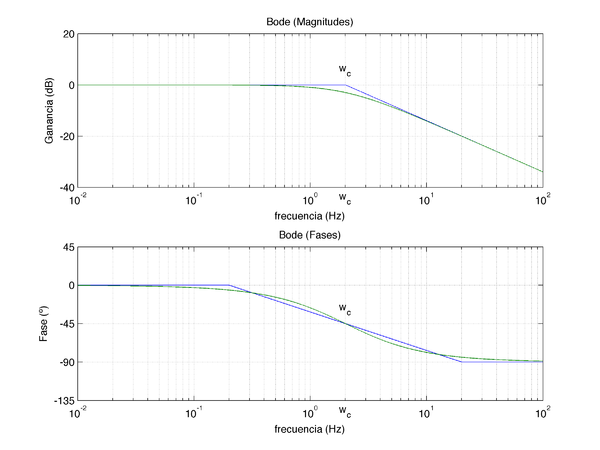
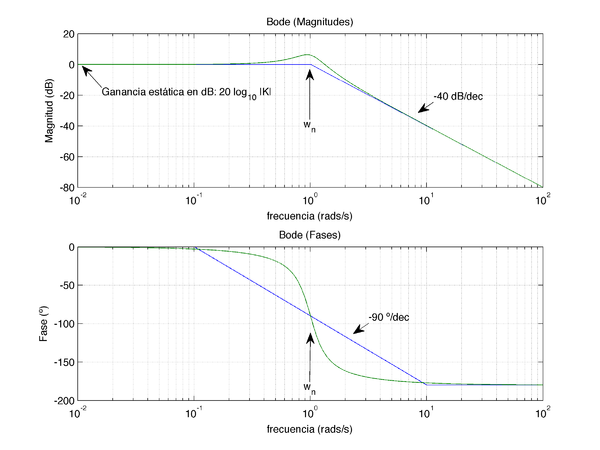
Dado su carácter dinámico, los sistemas se comportarán de formas diferentes ante senoides de distintas frecuencias (las ganancias y desfases variarán). El diagrama de Bode es, precisamente, una especie de radiografía de esa variación. En la figura adjunta se muestran los diagramas de Bode (reales y asintóticos) de sistemas de primer y segundo orden, respectivamente:

Bode de un sistema de primer orden (verde=real, azul=asintótico).

Bode de un sistema de segundo orden (verde=real, azul=asintótico).

Para trazar adecuadamente el diagrama de Bode experimental es necesario calcular varios puntos (en realidad, cuantos más se calculen, mejor aproximación tendremos). Repetir los pasos anteriores para distintas frecuencias.

Primer orden

• Obtener la ganancia y fase para al menos cuatro frecuencias:

1. En continua (w=0). Hallar la ganancia estática del sistema L(0) aplicando continua o frecuencias muy bajas, donde el desfase entre las senoides de salida y entrada es casi cero
2. Frecuencia de corte ω_c. Buscar la frecuencia a la que el desfase es de -45º y la ganancia es de -3 dB. Dicha frecuencia coincide con la frecuencia de corte ω_c = 1 / T. Esta frecuencia define el ancho de banda del sistema de primer orden y en ella el diagrama asintótico tiene un codo en el que la pendiente pasa de 0 dB/década a -20 dB/década.
3. Frecuencia baja. Elegir aproximadamente a ω_c / 5
4. Frecuencia alta. Elegir aproximadamente a 5ω_c
5. Frecuencia muy alta. Elegir una frecuencia 10 ó 20 veces superior a la frecuencia de corte.

Segundo orden

• Obtener la ganancia y fase para al menos cuatro frecuencias:

1. En continua (w=0). Hallar la ganancia estática del sistema L(0) aplicando continua o frecuencias muy bajas, donde el desfase entre las senoides de salida y entrada es casi cero
2. Frecuencia de oscilación natural ω_n. Buscar la frecuencia a la que el desfase es de -90º. La ganancia en este caso puede ser muy variable y dependerá de la amortiguación del sistema ξ. A esta frecuencia el diagrama asintótico tiene un codo en el que la pendiente pasa de 0 dB/década a -40 dB/década.
3. Frecuencias baja. Elegir aproximadamente ω_n / 5 para el de segundo orden
4. Frecuencia alta. Elegir aproximadamente 5ω_n para el de segundo orden
5. Frecuencia muy alta. Elegir una frecuencia 10 o 20 veces superior a la frecuencia de oscilación natural.

Hoja de resultados

A continuación se adjunta una tabla para anotar los datos experimentales y dos plantillas para el trazado del diagrama de Bode de los sistemas de primer y segundo orden. Descargarlas e imprimirlas para realizar la práctica.

Tabla de datos

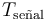
	$T_{\rm se\tilde nal}$	Tretardo	upp	ypp	ω (rads/s)	Φ (º)	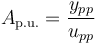$A_{\rm p.u.}=\frac{y_{pp}}{u_{pp}}$	$A_{\rm dB}=20 \log_{10}\left|\frac{y_{pp}}{u_{pp}}\right|$
Punto 1:
Punto 2:
Punto 3:
Punto 4:
Punto 5:
Punto 5:
Punto 6:
Punto 7:
Punto 8:
Punto 9:
Punto 10:

Diagrama de Bode del sistema de Primer Orden

Diagrama de Bode del sistema de Segundo Orden