Introducción al Laboratorio de Sistemas Continuos
m (→Objetivos) |
m (→Ejercicio 1. Respuesta al escalón de sistemas de primer y segundo orden) |
||
| (No se muestran 7 ediciones intermedias realizadas por un usuario) | |||
| Línea 13: | Línea 13: | ||
== Desarrollo de la práctica == | == Desarrollo de la práctica == | ||
| − | === Ejercicio 1. Respuesta al escalón de | + | === Ejercicio 1. Respuesta al escalón de sistemas de primer y segundo orden === |
==== Montaje ==== | ==== Montaje ==== | ||
| − | Insertar en la base de conexiones la fuente de alimentación y un módulo de primer orden. Conectar mediante uno de los cables suministrados la salida de la fuente de alimentación a la entrada del sistema | + | Insertar en la base de conexiones la fuente de alimentación y un módulo (sistema de primer o de segundo orden). Conectar mediante uno de los cables suministrados la salida de la fuente de alimentación a la entrada del sistema. Para realizar las medidas con el osciloscopio, conectar el cocodrilo de la masa del osciloscopio en las bornas de masa de la base de conexión, o en las de la fuente de alimentación (todas están unidas internamente). Los capuchones de las sondas deberán conectarse a la entrada y a la salida del sistema respectivamente. |
====Objetivos==== | ====Objetivos==== | ||
El alumno deberá realizar las siguientes tareas: | El alumno deberá realizar las siguientes tareas: | ||
| − | * | + | * Para los sistemas de primer y segundo orden: |
<math>G(s) = \frac{K}{1+Ts}</math> | <math>G(s) = \frac{K}{1+Ts}</math> | ||
| + | <math>G(s) = \frac{K \omega^2_n}{s^2+2\xi\omega_n s + \omega^2_n}</math> | ||
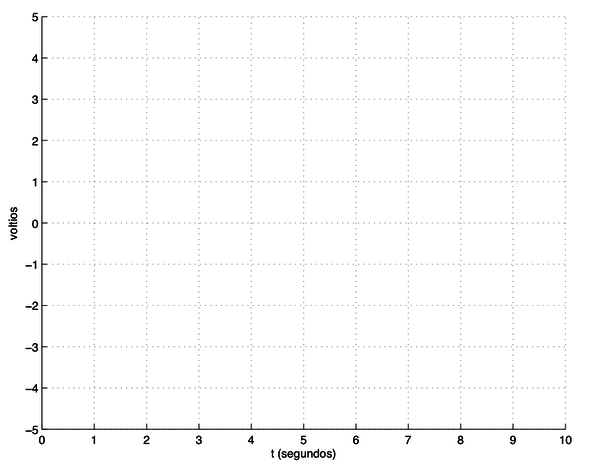
* Visualizar en el osciloscopio la entrada aplicada y la respuesta ante un escalón (puede hacerse empleando una señal cuadrada de frecuencia baja). Registrar en un gráfico cuadriculado, de forma aproximada, la respuesta experimental obtenida midiendo mediante el osciloscopio. Puede utilizarse si se quiere la plantilla adjunta: | * Visualizar en el osciloscopio la entrada aplicada y la respuesta ante un escalón (puede hacerse empleando una señal cuadrada de frecuencia baja). Registrar en un gráfico cuadriculado, de forma aproximada, la respuesta experimental obtenida midiendo mediante el osciloscopio. Puede utilizarse si se quiere la plantilla adjunta: | ||
| + | |||
[[image:plantilla-respuesta-temporal.png|center|600px]] | [[image:plantilla-respuesta-temporal.png|center|600px]] | ||
| − | * | + | |
| + | |||
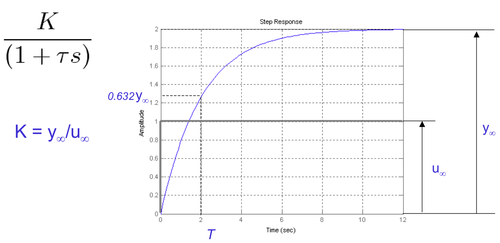
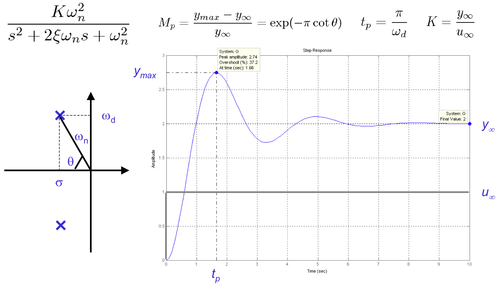
| + | * Identificar el sistema contrastando los parámetros típicos de la respuesta teórica (<math>K</math>, <math>T</math>, <math>t_p</math>, <math>M_p</math>, etc., ver figuras adjuntas) con las de la respuesta experimental y obtener de forma aproximada la función de transferencia ''G(s)'' del sistema. | ||
| + | [[Image:IdentificacionPrimerOrden.png|thumb|center|500px|Identificación de un sistema de primer orden a partir de la respuesta al escalón]] | ||
| + | [[Image:IdentificacionSegundoOrden.png|thumb|center|500px|Identificación de un sistema de segundo orden a partir de la respuesta al escalón]] | ||
| + | |||
* A partir de la ''G(s)'' experimental obtenida en el punto anterior, simular en Matlab, utilizando la función <code>lsim()</code>, la respuesta del sistema ante la misma entrada. Cotejar la respuesta simulada con la respuesta real. | * A partir de la ''G(s)'' experimental obtenida en el punto anterior, simular en Matlab, utilizando la función <code>lsim()</code>, la respuesta del sistema ante la misma entrada. Cotejar la respuesta simulada con la respuesta real. | ||
Última revisión de 12:36 11 dic 2007
Tabla de contenidos |
[editar] Características de la práctica
[editar] Duración
Dos horas aproximadamente
[editar] Requisitos previos
Para realizar adecuadamente esta práctica es conveniente:
- Conocer los principios básicos de manejo de un osciloscopio. Puede ayudar la siguiente información Introducción al manejo del osciloscopio
- Conocer las características de los equipos de prácticas. En la página Introducción al los módulos de prácticas puedes encontrar una descripción resumida.
- Haber estudiado la dinámica de sistemas de primer y segundo orden.
[editar] Desarrollo de la práctica
[editar] Ejercicio 1. Respuesta al escalón de sistemas de primer y segundo orden
[editar] Montaje
Insertar en la base de conexiones la fuente de alimentación y un módulo (sistema de primer o de segundo orden). Conectar mediante uno de los cables suministrados la salida de la fuente de alimentación a la entrada del sistema. Para realizar las medidas con el osciloscopio, conectar el cocodrilo de la masa del osciloscopio en las bornas de masa de la base de conexión, o en las de la fuente de alimentación (todas están unidas internamente). Los capuchones de las sondas deberán conectarse a la entrada y a la salida del sistema respectivamente.
[editar] Objetivos
El alumno deberá realizar las siguientes tareas:
- Para los sistemas de primer y segundo orden:
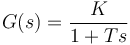
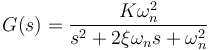
- Visualizar en el osciloscopio la entrada aplicada y la respuesta ante un escalón (puede hacerse empleando una señal cuadrada de frecuencia baja). Registrar en un gráfico cuadriculado, de forma aproximada, la respuesta experimental obtenida midiendo mediante el osciloscopio. Puede utilizarse si se quiere la plantilla adjunta:
- Identificar el sistema contrastando los parámetros típicos de la respuesta teórica (K, T, tp, Mp, etc., ver figuras adjuntas) con las de la respuesta experimental y obtener de forma aproximada la función de transferencia G(s) del sistema.
- A partir de la G(s) experimental obtenida en el punto anterior, simular en Matlab, utilizando la función
lsim(), la respuesta del sistema ante la misma entrada. Cotejar la respuesta simulada con la respuesta real.
[editar] Ejercicio 2. Respuesta ante una señal senoidal
[editar] Montaje
Manteniendo el mismo montaje anterior, conmutar el selector de forma de onda en la fuente de alimentación a señales senoidales.
[editar] Objetivos
El objetivo de este ejercicio es introducir al alumno de forma descriptiva el concepto de respuesta frecuencial. Para el mismo sistema de primer orden, el alumno deberá realizar las siguientes tareas:
- Introducir una señal senoidal en el sistema. Visualizar la entrada y la salida. Medir de forma aproximada la amplitud de entrada Au y la amplitud de salida Ay. Medir de forma aproximada el desfase en grados φy − φu entre ambas senoides.
- Variar la frecuencia de la señal senoidal y repetir las medidas. ¿Qué ocurre con la relación entre las amplitudes
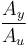 ? ¿Qué ocurre con el desfase φy − φu?
? ¿Qué ocurre con el desfase φy − φu?
- Dar una explicación a lo observado.
- Repetir con un sistema de segundo orden.