Contar el número de dientes de un engranaje

Contents

Cargamos la imagen y la convertimos a escala de gris

img=imread('176.jpg');
img=rgb2gray(img);

Seleccionamos un umbral y binarizamos la imagen

imhist(img)
% Se invierte el resultado para que el objeto quede blanco
img2=~im2bw(img,100/255);
imshow(img2);

Rellenamos los agujeros de los objetos encontrados

img3=imfill(img2,'holes');
imshow(img3);

Calculamos la diferencia

img4=imabsdiff(img3,img2);
imshow(img4)

Trazamos el contorno

[B,L] = bwboundaries(img4,'noholes');

figure; plot(B{1}(:,1),B{1}(:,2));

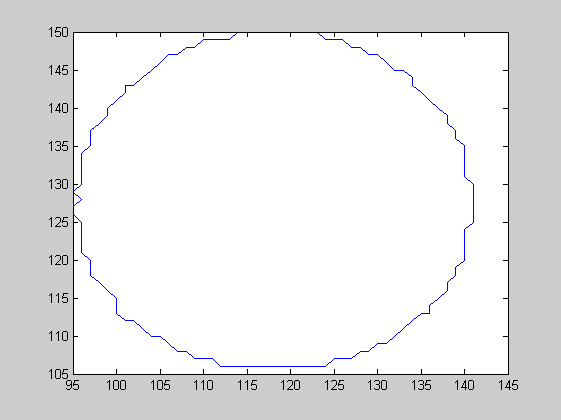
Ajustamos los datos del contorno a una circunferencia

% La ecuación básica de la circunferencia es:
% (x-xc)^2 + (y-yc)^2 = r^2,
% donde (xc,yc) es el centro y r es el radio.
%
% Dicha ecuación puede reescribirse en términos de tres parámetros a, b y c:
% x^2 + y^2 + a*x + b*y + c = 0,
% donde a = -2*xc, b = -2*yc, y c = xc^2 + yc^2 - r^2
%
% Matricialmente puede escribirse como:
% [x y 1] * [a b c]' = -[x^2+y^2]
% donde x e y son las coordenadas de cada uno de los puntos del contorno que
% queremos aproximar por una circunferencia
%
% Resolvemos un sistema de ecuaciones para poder calcular el valor de a, b y c
% A partir de ellos se calcularán las coordenadas del centro y el radio.

x = B{1}(:,2);
y = B{1}(:,1);

% Resolvemos el sistema de ecuaciones
abc = pinv([x y ones(length(x),1)])*(-(x.^2+y.^2));
a = abc(1); b = abc(2); c = abc(3);

% calculamos las coordenadas del centro y el radio
xc=-a/2;
yc=-b/2;
r=sqrt((xc^2+yc^2)-c)

% Marcamos el centro
imshow(img);
hold on;
plot(xc,yc,'rx','LineWidth',2);

% Dibujamos la circunferencia
theta = 0:0.01:2*pi;

% use parametric representation of the circle to obtain coordinates
% of points on the circle
Xfit = r*cos(theta) + xc;
Yfit = r*sin(theta) + yc;

plot(Xfit, Yfit,'r','LineWidth',2);

resultado = sprintf('xc:%2.3f yc:%2.3f r:%2.3f pixels', xc,yc,r);
text(15,15,resultado,'Color','r','FontWeight','bold');
%hold off;

r =

   22.5033

A partir de las características de las regiones.

% También es posible hacer el cálculo a partir de los valores calculados para
% las características de los objetos
[imgL,numobj]=bwlabel(img4,8);

% Calculamos las propiedades de las regiones
propiedades=regionprops(imgL, {'Centroid', 'EquivDiameter'});

xc=propiedades(1).Centroid(1);
yc=propiedades(1).Centroid(2);
r=propiedades(1).EquivDiameter/2;

% Marcamos el centro
%imshow(img);
%hold on;
plot(xc,yc,'gs','LineWidth',2);

% use parametric representation of the circle to obtain coordinates
% of points on the circle
Xfit = r*cos(theta) + xc;
Yfit = r*sin(theta) + yc;

plot(Xfit, Yfit,'g','LineWidth',2);

resultado = sprintf('xc:%2.3f yc:%2.3f r:%2.3f pixels', xc,yc,r);
text(15, size(img,1)-15,resultado,'Color','g','FontWeight','bold');
%hold off;

Published with MATLAB® 7.6