Ejercicio del martes 4 de Marzo de 2008 (Linealización)

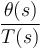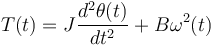1- Linealizar el sistema dado por las ecuaciones (1) y (2) y sacar la función de transferencia $\frac{\theta(s)}{T(s)}$.

$T(t) = J\frac{d^2\theta(t)}{dt^2} + B \omega^2(t)$ (1)

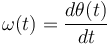$\omega(t) = \frac{d\theta(t)}{dt}$ (2)

donde J = 1, B = 1 y el punto de equilibrio viene dado por ω₀ = {última cifra del DNI}.

---

Solución:

Linealizamos la primera ecuación:

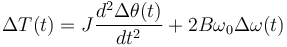$\Delta T(t) = J\frac{d^2\Delta\theta(t)}{dt^2} + 2 B \omega_0 \Delta\omega(t)$ (1')

La segunda ecuación ya es lineal:

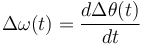$\Delta\omega(t) = \frac{d\Delta\theta(t)}{dt}$ (2')

Pasando ambas ecuaciones a transformadas de Laplace:

T(s) = Js²θ(s) + 2Bω₀ω(s) (3)

ω(s) = sθ(s) (4)

A partir de (3):

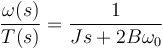$\frac{\omega(s)}{T(s)} = \frac{1}{J s + 2 B \omega_0 }$ (5)

A partir de (4):

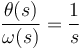$\frac{\theta(s)}{\omega(s)} = \frac{1}{s}$ (6)

Combinando (5) y (6):

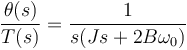$\frac{\theta(s)}{T(s)} = \frac{1}{s (J s + 2 B \omega_0) }$ (7)

Por ejemplo, para un DNI finalizado en 4, la solución sería:

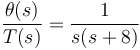$\frac{\theta(s)}{T(s)} = \frac{1}{s (s + 8) }$ (8)

---

2- Linealizar la ecuación (1) en el punto de equilibrio dado por x₀ = π / 2:

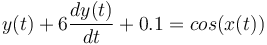$y(t) + 6\frac{dy(t)}{dt} + 0.1 = cos(x(t))$ (1)

---

Solución:

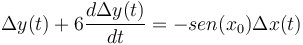$\Delta y(t) + 6\frac{d\Delta y(t)}{dt} = -sen(x_0)\Delta x(t)$ (1')

Como sen(x₀) = 1:

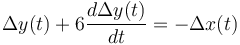$\Delta y(t) + 6\frac{d\Delta y(t)}{dt} = -\Delta x(t)$ (2)