Manejo de Sisotool en Matlab

¿Para qué sirve sisotool?

Sisotool es una herramienta gráfica que permite el análisis de sistemas lineales. En el presente manual se explica el manejo de esta herramienta para obtener y analizar el lugar de las raíces de un sistema. Lo haremos con un ejemplo sencillo:

---

Para un sistema cuya función de transferencia en lazo abierto es

$G(s) = \frac{1}{s+2}$

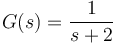
queremos dibujar el lugar de las raíces, es decir, el lugar geométrico que describen los polos del sistema en lazo cerrado para distintos valores de K. Esto equivale a determinar el lugar geométrico de las soluciones de la ecuación característica cuando varía K:

$1 + K\cdot G(s) = 0$

---

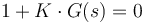
Llamada a la herramienta sisotool

En primer lugar, definimos la función de transferencia del sistema:

>> s = tf('s'); G = 1/(s+2),
 
Transfer function:
  1
-----
s + 2
 
>> 

Para llamar a la herramienta sisotool utilizamos el comando del mismo nombre

>> sisotool(G)
>> 

Elementos de la ventana principal de sisotool

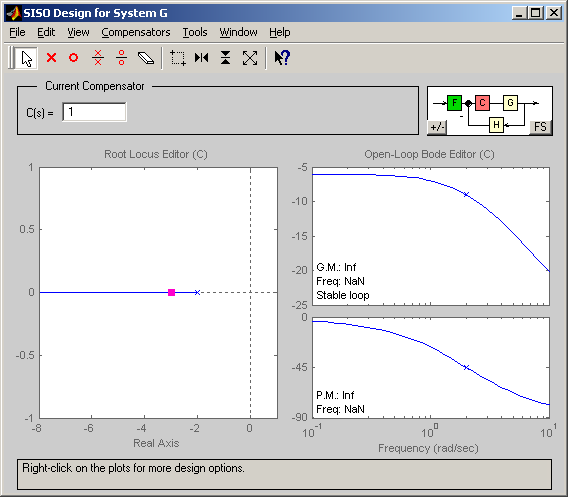
La ventana del sisotool nos muestra a la izquierda el lugar de las raíces del sistema G(s) cuando lo realimentamos. A la derecha nos muestra el diagrama de Bode en cadena abierta, tanto de amplitud como de fase, correspondiente a la ganancia indicada en la ventana 'Current compensator' ('controlador actual').

Los polos y ceros del sistema en cadena abierta se muestran como $\times$ y $\circ$ respectivamente. Los polos en cadena cerrada se muestran como cuadrados $\square$. En el ejemplo de la figura, realimentando el sistema G(s), con un regulador proporcional de ganancia uno ('Current compensator'), nos daría un polo en cadena cerrada en -3. El lugar de las raíces es una línea que parte del polo en cadena abierta y termina en $-\infty$.

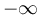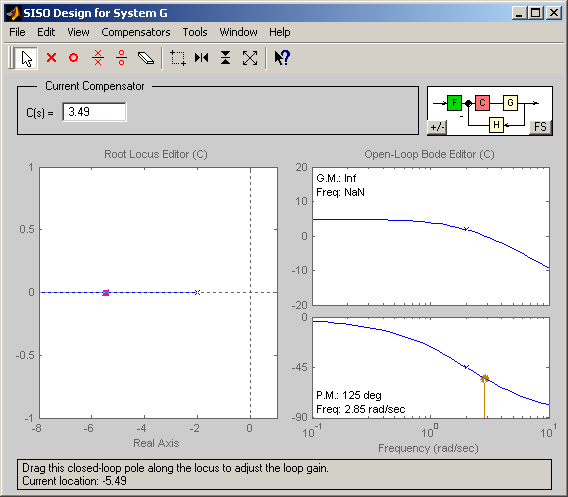
Modificación de la ganancia del controlador

Si queremos ver qué posición toman los polos en cadena cerrada cuando variamos la ganancia lo podemos hacer cambiando el valor de la ganancia del controlador. En este caso, al variar la ganancia a 3.49, cambia automáticamente la posición del polo en cadena cerrada. Otra opción es arrastrar el polo en cadena cerrada hasta la posición deseada, y que sisotool calcule el valor de la ganancia para que en cadena cerrada el polo tome esa posición.

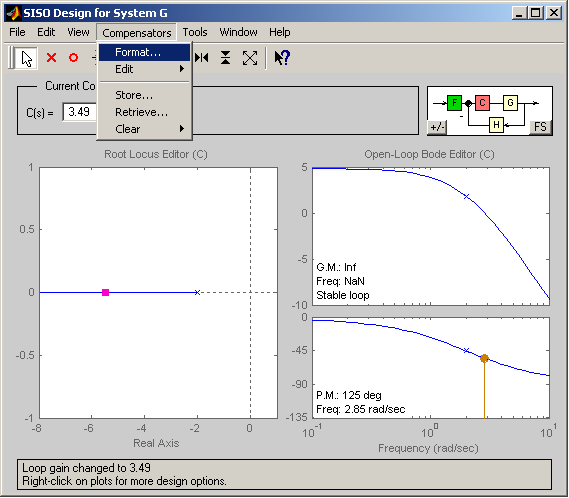
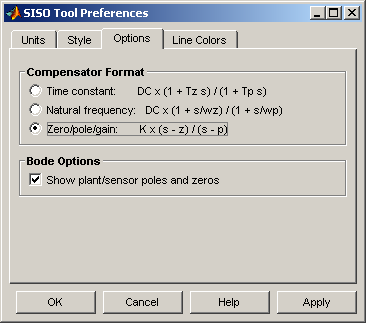
Representación factorizada del controlador

Como puede verse, en la parte superior de las figuras anteriores aparece la función de transferencia del controlador para la situación actual definida para la ganancia, polos y ceros del controlador, de la que resultan los polos en lazo cerrado descritos por los cuadrados $\square$ de color fucsia. Una opción interesante es hacer que la función de transferencia del controlador aparezca en formato ceros-polos-ganancia, donde numerador y denominador aparecen factorizados y en formato mónico (común cuando se utiliza el lugar de las raíces). Esto puede hacerse como se muestra en las siguientes figuras.

Visualización de respuestas del sistema

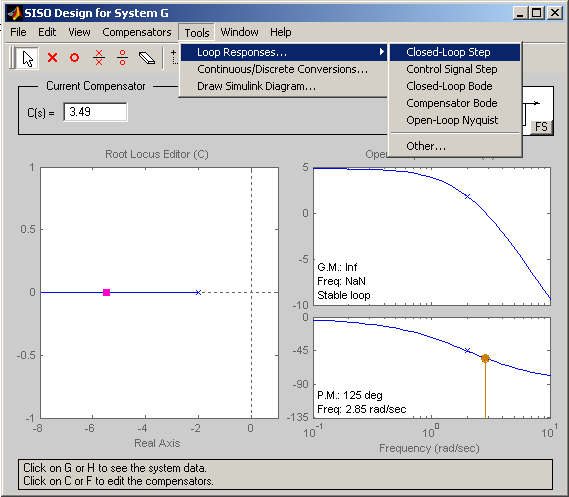
La herramienta sisotool también nos permite obtener las respuestas en lazo cerrado del sistema realimentado resultante. Hay varias posibilidades, pudiendo definirse cada una de eligiendo la entrada (referencia, perturbación, etc.), la salida (acción de control, señal de error, salida del proceso) así como el tipo de representación (Bode, respuesta al escalón, respuesta impulsional, Nyquist, etc.). En la figura siguiente se muestra la forma de obtener la respuesta al escalón en bucle cerrado:

Edición numérica del controlador

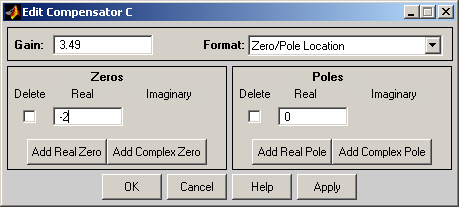
También es posible editar directamente el controlador, definiendo numéricamente la ganancia, los polos y los ceros accediendo a la opción edit compensator. A esta ventana se puede acceder haciendo doble click sobre el área que contiene al regulador.

Selección interactiva del controlador

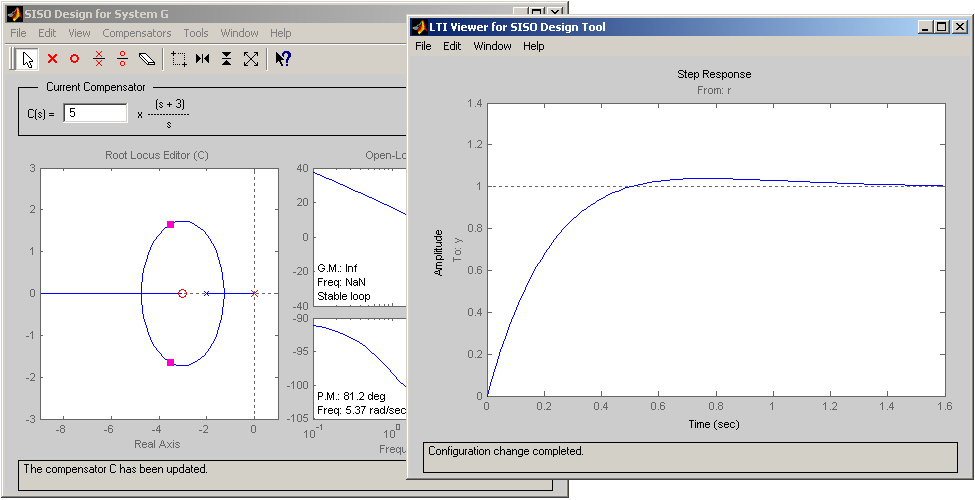
En la figura de abajo se muestra, finalmente, el lugar de las raíces para el controlador 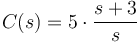$C(s) = 5\cdot \frac{s+3}{s}$ (ventana de la izquierda) junto con la respuesta al escalón (ventana de la derecha). En este punto, es posible "arrastrar" las raíces (cuadrados fucsia) por el lugar, lo que produce un cambio automático en la ganancia del controlador. También se pueden arrastrar el polo y el cero del controlador, lo que produce una modificación en la geometría del lugar de las raíces. En ambos casos, los "arrastres" producen también el cambio de la respuesta al escalón en el LTI viewer (ventana de la derecha). Además, en el LTI viewer, es posible obtener propiedades de la respuesta (valores de pico, valor en régimen permanente, etc.) pulsando en el botón derecho del ratón. Si hubiésemos definido cualquier otra respuesta (respuesta en frecuencia de una función de sensibilidad, por ejemplo, también reflejaría de forma simultánea los cambios). Esto permite analizar de forma interactiva las consecuencias de los cambios en nuestro diseño.

Introducción de restricciones al diseño

Menú desplegable mostrando la restricción del tiempo de establecimiento.

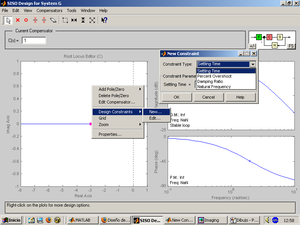
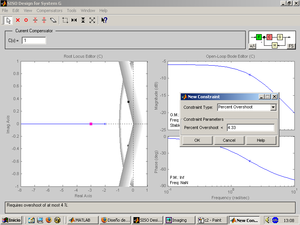
Pulsando el botón derecho del ratón sobre la ventana del lugar de las raíces, es posible introducir restricciones a nuestro diseño. En la primera figura de la derecha, puede verse el menú desplegable mostrando la restricción de tiempo de establecimiento.

Introducción de la especificación de M_p. Las restricciones que ya hay dibujadas corresponden a w_n inferior a 1 rad/s y sobreoscilación M_p inferior al 4%.

En el segundo ejemplo de la derecha, se han establecido dos restricciones para definir gráficamente la zona del plano S correspondiente a una frecuencia natural de oscilación w_n inferior a 1 rad/s y sobreoscilación M_p inferior al 4%.