Modelado de un motor CC

Introducción

El objetivo de la práctica es modelar el comportamiento de un sistema de servoposicionamiento basado en un motor de corriente continua. Un sistema de servoposicionamiento de continua consta de tres subsistemas: el eléctrico, el magnético y el mecánico.

Modelado matemático

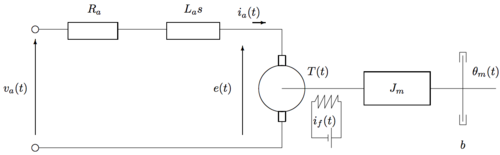
El esquema de un motor CC puede observarse en la figura adjunta

Esquema del motor

Subsistema magnético

Una de las partes más importantes del motor, el devanado de inducido, consiste en un arrollamiento de varias espiras que puede girar inmerso en un campo magnético constante. Dicho campo magnético puede ser generado por un imán permanente o por un devanado de excitación consistente en una bobina por la que circula una corriente de excitación i_f(t), que supondremos constante para que el campo sea también constante. Al circular una corriente i_a(t) por el devanado de inducido, como resultado de la interacción con el campo magnético se ejerce sobre él un par T(t) que es directamente proporcional al campo magnético y a la propia corriente de inducido i_a(t). Dado que hemos supuesto el campo magnético constante, el par motor será proporcional a la corriente de inducido

T(t) = Kt.ia(t)

(1)

Por otra parte, el giro de las espiras del devanado de inducido en presencia del campo magnético, produce en bornas del mismo una caída de tensión o fuerza contraelectromotriz, e(t), proporcional a su velocidad de giro

$e(t) = K_e . \dot \theta_m(t)$

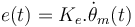
(2)

Subsistema eléctrico

Asimismo, el devanado de inducido es, a todos los efectos, un conductor, con una resistencia R_a y una inductancia L_a, sobre el que hay que considerar, además, la fuerza contraelectromotriz como una fuente de tensión dependiente de la velocidad de giro. La ecuación en la malla de inducido será, por tanto:

$v_a(t) = R_a\cdot i_a(t) + L_a\cdot \frac{di_a(t)}{dt} + K_e\cdot \dot\theta_m(t)$

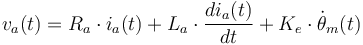
(3)

Aplicando la transformada de Laplace a la ecuación eléctrica se tiene

Va(s) = (Ra + sLa)Ia(s) + KesΘm(s)

(4)

Subsistema mecánico

El par mecánico T(t) desarrollado por el motor se emplea para imprimir aceleración angular 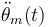$\ddot \theta_m(t)$ a la carga y en vencer la fuerza de fricción 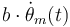$b\cdot \dot \theta_m(t)$ (la fricción viscosa es aproximadamente proporcional a la velocidad de giro):

$T(t) = J_m\cdot \ddot \theta_m(t) + b\cdot \dot \theta_m(t)$

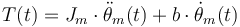
(5)

Aplicando la transformada de Laplace a la ecuación anterior y teniendo en cuenta que la velocidad angular Ω_m(s) = sΘ_m(s) se tiene:

$T(s) = (J_ms + b) \cdot \Omega_m(s)$

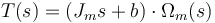
(6)

Función de transferencia

Agrupando términos, la función de transferencia que relaciona la tensión de inducido con la posición angular es

$\frac{\Theta_m(s)}{V_a(s)} = \frac{K_t}{s[(J_m s + b)(L_a s + R_a) + K_t K_e]}$

(7)

Objetivos

El alumno deberá entregar un informe con los siguientes puntos:

• Teniendo en cuenta las ecuaciones del subsistema eléctrico, (4), las del subsistema magnético, (1) y (2), y la del subsistema mecánico (6), obtener el diagrama de bloques del motor, considerando la tensión aplicada al inducido, V_a(s), como entrada, y la posición angular, Θ_m(s), como salida. Indicar sobre el diagrama los tres principales subsistemas dinámicos que lo componen (mecánico, magnético y eléctrico) y el flujo de señales entre éstos.
• Deducir a partir del diagrama de bloques las funciones de transferencia entre la tensión de inducido v_a(t) (entrada) y las variables θ_m(t), ω_m(t), i_a(t) (salidas)
• Utilizando la función step(), trazar en sendas figuras de MATLAB la evolución de la velocidad angular ω_m(t), la posición angular θ_m(t) y la corriente consumida por el motor i_a(t), cuando se aplica un escalón de 133 voltios en bornes del inducido.

• Repetir el apartado anterior cuando se aplica una tensión de inducido senoidal 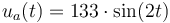$u_a(t) = 133\cdot \sin(2t)$. Utilizar la función lsim(), que permite simular un sistema lineal ante cualquier tipo de entrada.

Bibliografía y enlaces

• Franklin et al. Feedback Control of Dynamic Systems 5ª Edición, Ed. Prentice Hall. Puede encontrarse un desarrollo similar del modelo del motor CC al de la práctica en el ejemplo 2.11, pp. 42-43. La nomenclatura de la práctica ha sido adaptada a este ejemplo para que el alumno tenga una referencia en el libro de la asignatura.

• Franklin et al. Feedback Control of Dynamic Systems 5ª Edición, Ed. Prentice Hall. En la sección 3.2 (System modelling diagrams, pp. 102-106) explica con bastante detalle y con ejemplos los procedimientos básicos necesarios para trabajar con diagramas de bloques, que te serán útiles para desarrollar algunos de los puntos de la práctica.

• CTM: Control Tutorials for Matlab. Página web de la Universidad de Michigan con tutoriales paso a paso de modelado de sistemas y control mediante Matlab.

Apéndices

Ejemplo básico de MATLAB

Utiliza este ejemplo como plantilla. Copia y pega código donde necesites para resolver la práctica.

 % Definimos la función de transferencia usando tf(num,den)
 G = tf([1 2],[1 2 3]),


 % RESPUESTA ANTE UN ESCALÓN ENTRE t=0 y t=10
 figure(1);
 t = linspace(0,10,1000);
 step(G,t);
 grid on;                    % dibuja una retícula

 % RESPUESTA ANTE UN IMPULSO ENTRE t=0 y t=10
 figure(2);
 t = linspace(0,10,1000);
 impulse(G,t);
 grid on;                    % dibuja una retícula



 % RESPUESTA ANTE UNA SEÑAL CUALQUIERA 
 figure(3);

 A = 2;      % amplitud de la senoide
 phi = 0;    % fase de la senoide
 f   = 0.2;  % frecuencia de la senoide

 % Para trabajar con una señal cualquiera u(t) hay que definir un vector de 
 % tiempos y otro vector con los valores que toma dicha señal en cada uno 
 % de esos instantes de tiempo
 t = linspace(0,10,1000);        % vector de tiempos
 u = A*sin(2*pi*f*t + phi);      % vector de datos
 y = lsim(G,u,t);        % simulamos el sistema definido por G para la entrada definida por u(t)


 % Dibujamos el resultado de la simulación
 plot(t,u,t,y);              % dibujamos u(t) e y(t) en una misma figura
 legend('entrada u(t)','salida y(t)');
 grid on;                    % dibuja una retícula
 title('Respuesta ante una señal u(t)');

Datos de la práctica

Los parámetros del motor, obtenidos de manera experimental, son (en unidades del Sistema Internacional):

Ra = 1.1648; La = 0.0068; Kt = 0.55; Ke = 0.82; b = 0.00776; Jm = 0.0271;

Nota: Para ahorrar tiempo puedes copiarlos y pegarlos en tu script de MATLAB