Simulación y animación del sistema de amortiguación de un vehículo

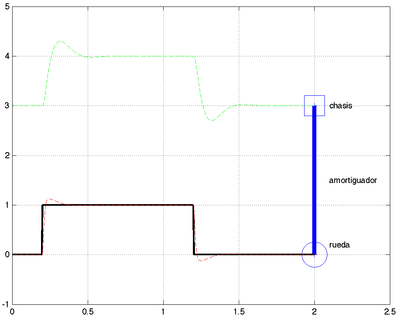
Siguiendo el ejemplo 2.2 del Franklin (pag. 25) hemos simulado el comportamiento del sistema utilizando Matlab y realizado una animación del comportamiento ante una situación específica (un bache). Puedes copiar el código y pegarlo directamente en Matlab para ver la animación y los resultados de la simulación. Pero si quieres aprender de verdad, lo ideal es que te lo trabajes algo más. Léete bien el ejemplo, haz a mano los desarrollos y dale vueltas a los conceptos que se manejan. Cuando lo entiendas bien, mete el código en un script de Matlab (archivo de texto *.m ejecutable desde la línea de comandos de Matlab) y "juega" con él, cambiando parámetros, y escenarios de la simulación.

Captura de la simulación del sistema de suspensión de un vehículo

Código en MATLAB

% EJEMPLO: SIMULACIÓN Y ANIMACIÓN DEL SISTEMA DE SUSPENSIÓN DE UN VEHÍCULO
%
% Basado en el Ejemplo 2.2 de Franklin (pp. 25 y ss.)
%
% ANÁLISIS DINÁMICO DE SISTEMAS (TELECO), EPS DE INGENIERÍA DE GIJÓN
% Área de Ingeniería de Sistemas y Automática


% PARAMETROS MECÁNICOS DEL VEHÍCULO
m_coche = 1580;                     % Masa total del vehículo (incluidas las 4 ruedas)
m_rueda = 20;                       % Masa de cada rueda
m2      = (m_coche - 4*m_rueda)/4;  % masa del chasis que le corresponde a cada rueda
m1      = m_rueda;                  % masa de la rueda
ks      = 130000;
kw      = 1000000;
b       = 9800;


% FUNCIONES DE TRANSFERENCIA
num = (kw*b)/(m1*m2)*[1 ks/b];
den = [1, (b/m1 + b/m2), (ks/m1 + ks/m2 + kw/m1), (kw*b)/(m1*m2), (kw*ks)/(m1*m2)];



G_yr = tf(num,den);                 % fdt entre la elevación de la carretera y la posicion del chasis
G_xr = G_yr*tf([m2 b ks],[b ks]);   % fdt entre la elevación de la carretera y la posición de la rueda


% PARAMETROS DE SIMULACION
N = 500;                            % Número de muestras (más muestras permiten un análisis más fino, 
                                    % pero más lento, ajustar ésto según la 
                                    % potencia del ordenador
t = linspace(0,2,N);
r = [zeros(1,N*0.1) ones(1,N*0.5) zeros(1,N*0.4)];  % elevación de la carretera
y = lsim(G_yr,r,t);                                 % posición relativa del chasis
x = lsim(G_xr,r,t);                                 % posición relativa de la rueda



% ANIMACIÓN A PARTIR DE LA SIMULACIÓN REALIZADA
for k = 1:length(t)
    clf;
    plot(t(k),y(k)+3,'s','markersize',30); hold on;
    text(t(k)+.1,y(k)+3,'chasis');
    text(t(k)+.1,(y(k)+3+x(k))/2,'amortiguador');       % sumamos una cantidad (ej. 3) para establecer la posición absoluta del chasis
    plot(t(k),y(k)+3,'+');     
    plot(t(k),x(k)+0,'o','markersize',30); 
    plot(t(k),x(k)+0,'+'); 
    text(t(k)+.1,x(k)+0.2,'rueda');
    plot([t(k) t(k)],[x(k),y(k)+3],'linewidth',5);
    plot(t,r,'k','linewidth',2); 
    plot(t(1:k),y(1:k)+3,'g--'); 
    plot(t(1:k),x(1:k)+0,'r--'); hold off;
    axis([0,t(end)+0.5,-1,5]);
    grid on;
    drawnow;                                            % Para la animación, forzamos el refresco de la figura en cada bucle
    
end


% EN OTRA FIGURA DIBUJAMOS LAS GRÁFICAS DE LA EVOLUCIÓN TEMPORAL DE CADA VARIABLE
figure(2);
subplot(3,1,1);
plot(t,r)
grid on;
title('elevación de la carretera');
subplot(3,1,2);
plot(t,x);
grid on;
title('posición de la rueda');
subplot(3,1,3);
plot(t,y);
grid on;
title('posición del chasis');