Perlas
De ISAwiki
(Diferencia entre revisiones)
| (No se muestran 17 ediciones intermedias realizadas por 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | + | A continuación se muestran algunas frases útiles para demostrar un desconocimiento profundo de los sistemas de control. | |
| + | Para respetar los derechos de autor, se mantienen las citas con su gramática y ortografía original. | ||
| + | |||
=== Análisis de estabilidad en c.a. y en c.c === | === Análisis de estabilidad en c.a. y en c.c === | ||
| − | * " | + | * "Que el sistema sea estable en c.a. implica que lo sea en c.c.". |
| − | + | ||
* "Si es estable en cadena abierta, aún más en cadena cerrada". | * "Si es estable en cadena abierta, aún más en cadena cerrada". | ||
| + | * "Un sistema en cadena abierta al no tener realimentación será inestable” | ||
| + | * "Cadena abierta: si es estable, ya que segun el teorema del valor final, la ganancia <math>\neq \infty</math>". | ||
| + | * "El sistema es estable en cadena abierta ya que tanto MG como MF son positivos". | ||
* "Se ve que <math>\omega_{cg}</math> < <math>\omega_{cf}</math> por lo tanto el sistema es estable en c.a." | * "Se ve que <math>\omega_{cg}</math> < <math>\omega_{cf}</math> por lo tanto el sistema es estable en c.a." | ||
| − | * " | + | * "En cadena cerrada también es estable ya que la realimentación es unitaria por tanto el MF y MG del sistema permanecen igual". |
| + | * "El sistema es estable en cadena cerrada por que el MG es positivo, el MF no influye ya que la estabilidad no depende de la frecuencia". | ||
| + | * "Es estable en cadena abierta porque el margen de fase es mayor que cero. Es estable en cadena cerrada porque el margen de ganancia es mayor que cero". | ||
| + | * "El sistema es estable ya que MF y MG son negativos. Sería estable tanto en cadena cerrada como en cadena abierta." | ||
| + | |||
| + | === Limitaciones fundamentales del control === | ||
| + | * ''Explique brevemente las consecuencias del Teorema de Bode''. | ||
| + | : "La consecuencia del '''diagrama de Bode''' es una representación independiente en 2 diagramas logarítmicos de la amplitud y la fase de la repuesta de un sistema, para poder obtener parámetros característicos de este sistema." | ||
| + | |||
| + | === Diseño de compensadores === | ||
| + | * "Si queremos una red de atraso de fase utilizamos un regulador PI. Este regulador introduce ceros en el sistema sin necesidad de introducir ningún polo". | ||
| + | |||
| + | == Errores == | ||
| + | *"Inicialmente tengo un sistema tipo 1. Si introduzco una entrada tipo escalón, incremento en 1 unidad el tipo <math>\rightarrow</math> Tendré tipo 2. | ||
| + | * "El sistema no tiene integradores en el origen" | ||
| + | |||
| + | ---- | ||
| + | |||
| + | * "Cuando aplicamos una señal de una frecuencia muy parecida a cero con A = 1, [y] el sistema [tiene] <math>G(j\omega)=1.5</math>, hay una ganancia de 0.5". | ||
Última revisión de 12:21 15 may 2014
A continuación se muestran algunas frases útiles para demostrar un desconocimiento profundo de los sistemas de control.
Para respetar los derechos de autor, se mantienen las citas con su gramática y ortografía original.
Tabla de contenidos |
[editar] Análisis de estabilidad en c.a. y en c.c
- "Que el sistema sea estable en c.a. implica que lo sea en c.c.".
- "Si es estable en cadena abierta, aún más en cadena cerrada".
- "Un sistema en cadena abierta al no tener realimentación será inestable”
- "Cadena abierta: si es estable, ya que segun el teorema del valor final, la ganancia
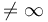 ".
".
- "El sistema es estable en cadena abierta ya que tanto MG como MF son positivos".
- "Se ve que ωcg < ωcf por lo tanto el sistema es estable en c.a."
- "En cadena cerrada también es estable ya que la realimentación es unitaria por tanto el MF y MG del sistema permanecen igual".
- "El sistema es estable en cadena cerrada por que el MG es positivo, el MF no influye ya que la estabilidad no depende de la frecuencia".
- "Es estable en cadena abierta porque el margen de fase es mayor que cero. Es estable en cadena cerrada porque el margen de ganancia es mayor que cero".
- "El sistema es estable ya que MF y MG son negativos. Sería estable tanto en cadena cerrada como en cadena abierta."
[editar] Limitaciones fundamentales del control
- Explique brevemente las consecuencias del Teorema de Bode.
- "La consecuencia del diagrama de Bode es una representación independiente en 2 diagramas logarítmicos de la amplitud y la fase de la repuesta de un sistema, para poder obtener parámetros característicos de este sistema."
[editar] Diseño de compensadores
- "Si queremos una red de atraso de fase utilizamos un regulador PI. Este regulador introduce ceros en el sistema sin necesidad de introducir ningún polo".
[editar] Errores
- "Inicialmente tengo un sistema tipo 1. Si introduzco una entrada tipo escalón, incremento en 1 unidad el tipo
 Tendré tipo 2.
Tendré tipo 2.
- "El sistema no tiene integradores en el origen"
- "Cuando aplicamos una señal de una frecuencia muy parecida a cero con A = 1, [y] el sistema [tiene] G(jω) = 1.5, hay una ganancia de 0.5".