en español
en español| Introduction | People | Gallery | Publications | Projects | Contact |
|---|
|
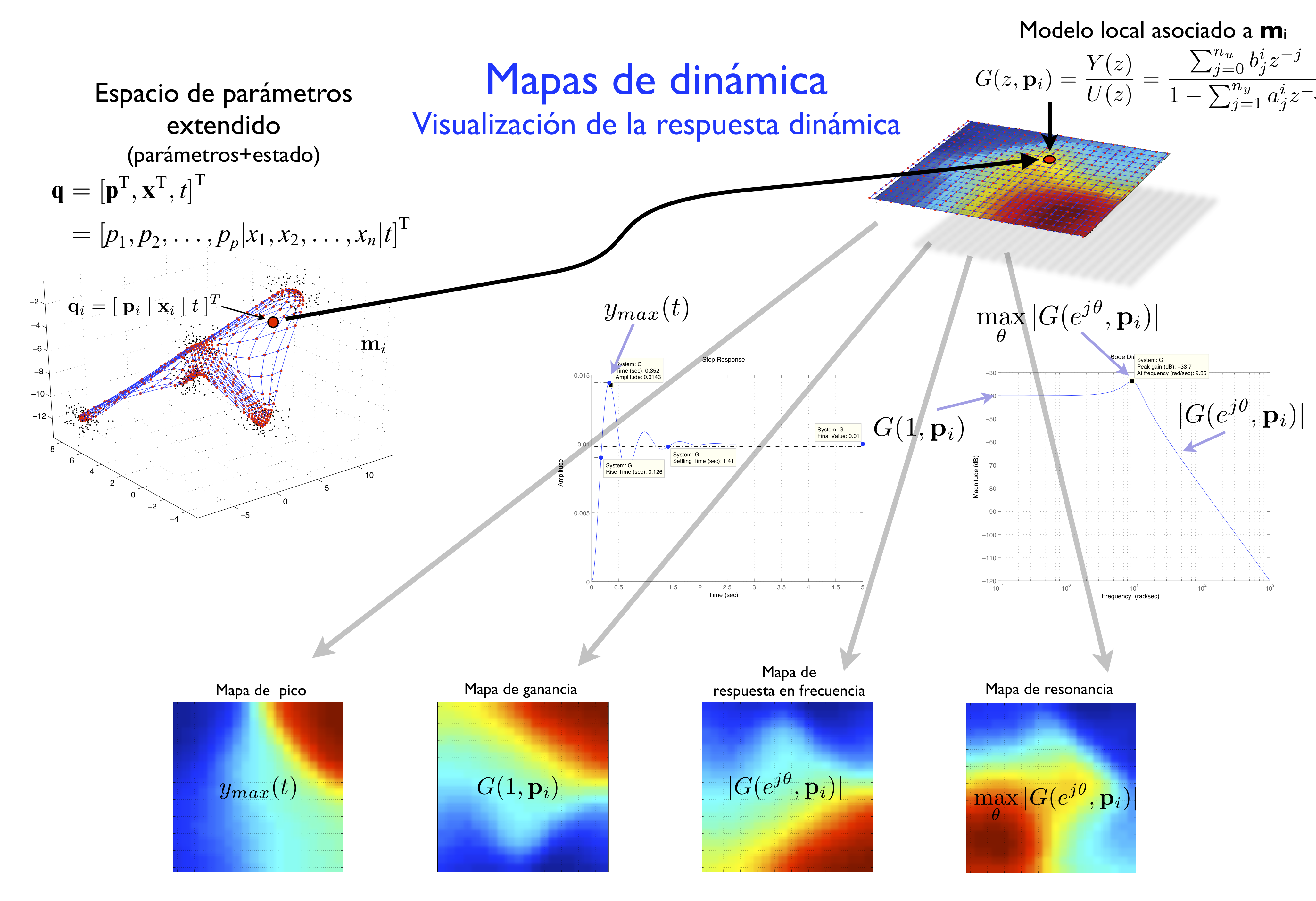
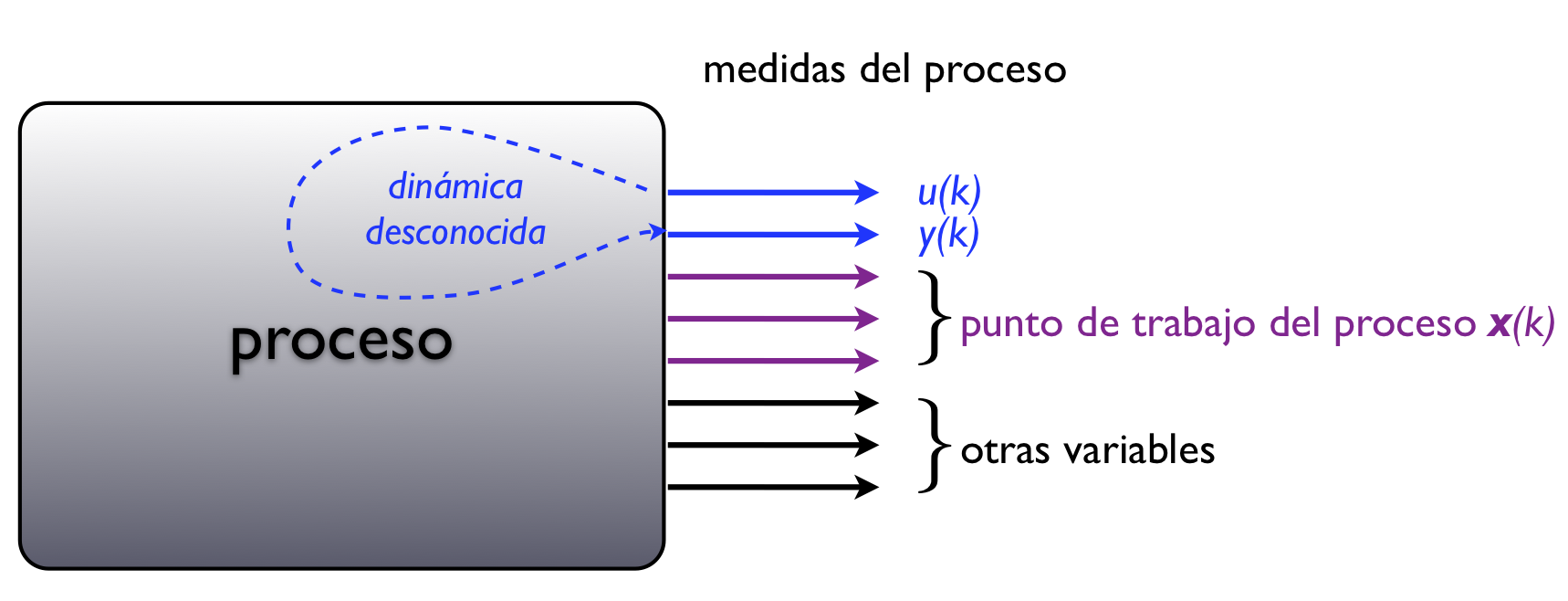
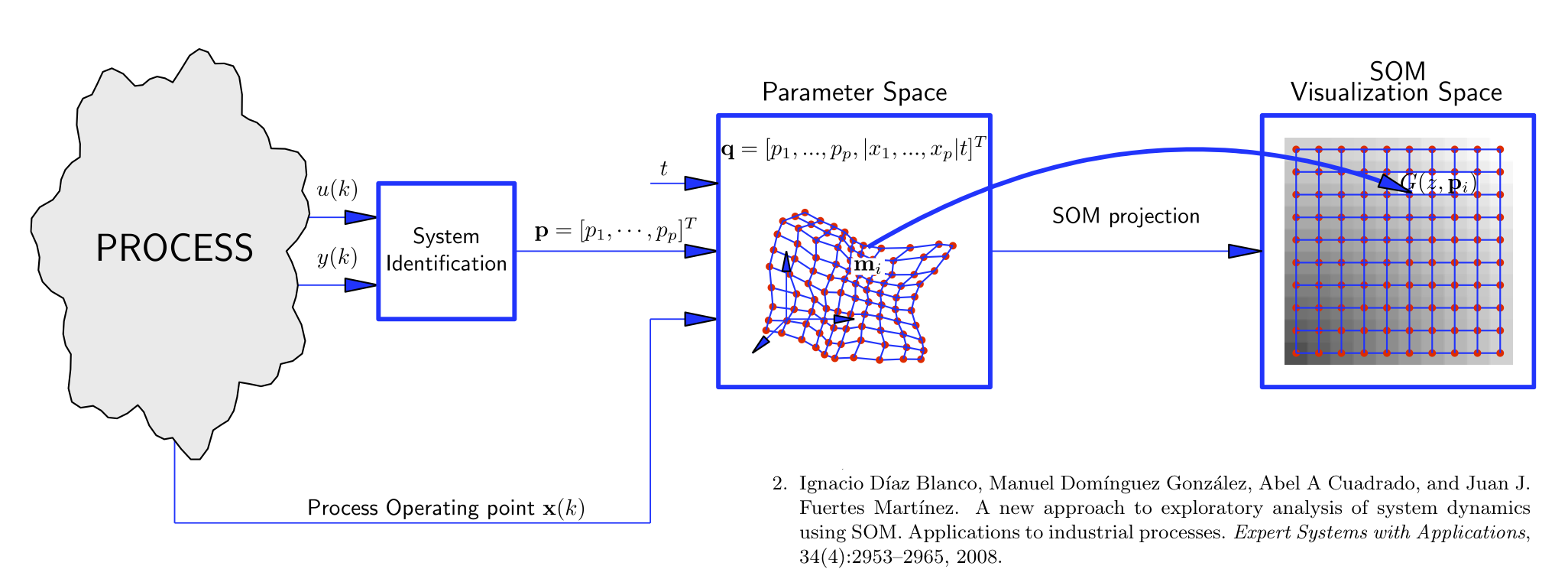
The Self-Organizing Map (SOM) is a powerful method for the exploratory analysis of process data, which is based on the dimensionality reduction principle. The SOM algorithm defines a smooth nonlinear mapping between a high dimensional input space and a low dimensional space (typically 2D) that preserves the relevant information about the input data distribution. this mapping can be used to obtain representations (typically 2D images) of the process variables \(x_1,\dots, x_n\), that can be seen as layers of a same map shoing different kinds of information, in a similar way as pressure, rain or temperature maps in a weather map. The resulting images (called "planes") can be mutually compared and hence they reveal the main relationships, allowing the user to exploit available knowledge about the process in a highly efficient way, by means of an exploratory analysis. Each point (i,j) of the 2D map is associated to a point \(\mathbf m_i\) in the input space called "prototype", with representative values for all the process variables in the input space, thereby defining a representative process state. An extension of the SOM projection, can be obtained by defining an extra set of parameters or descriptors \(p_1, p_2,\dots, p_p\) of a dynamic model. When projecting the points of this "extended" space by means of the SOM, new planes are generated where each point represents a prototype which contains both the operating point (process variables) and the local dynamic behavior of the process (parameters \(p_i\)). Thus, the SOM mapping establishes an association between the subspace of process variables which defines an operating point, and the paramters subspace, which defines the dynamic behavior, so the planes from both subspaces are mutually consistent and comparable one to each other. This allows the user to explore the influence relationships between a set of process variables (for instance, variables defining an operating point) and its local dynamic behavior, resulting in a useful way for the analysis of nonlinear and nonstationary processes. |
 |